The SEC announced the adoption of its new pay for performance rules, or Item 402(v) on August 25, 2022. A detailed summary of the new rules can be found within our Alert found here, or at www.SECPayVersusPerformance.com.
As a reminder, the new rules require all outstanding and unvested awards to be re-valued as of the end of the fiscal year and awards that vest during the fiscal year to be valued on their vest date. The incremental change in fair value from the end of the fiscal year (or vest date if sooner) as compared to the end of the prior fiscal year, is included as Compensation Actually Paid during the year. The guidance states “(3) Fair value amounts must be computed in a manner consistent with the fair value methodology used to account for share-based payments in the registrant’s financial statements under generally accepted accounting principles”. Therefore, it is critical to use a consistent process for pay for performance re-valuation to what was done on the grant date and disclosed in current financial reporting.
In Compensation Actually Paid and Stock Option Valuations (Part 1), we laid out several simplistic but practical approaches for developing an expected life for stock options, all with their own potential pros and cons. With this brief, we want to lay out a new thoughtful alternative that may be a better approximate for the expected life. As we’ll see below, compiling valuations using this methodology could potentially lead to reduced fair value estimates compared to other approaches. We also walk you through a case study and comparison of two companies with different grant dates to help illustrate the nuances of calculating expected life in accordance with the new rules.
Background
The majority of companies that use the Black-Scholes model for estimating the fair value of employee options and have a process to estimate the expected life of the options as of the grant date. However, the SEC’s new Pay vs. Performance rules require companies to estimate the fair value of unvested employee options at the end of each fiscal year and on their vest date as well. This introduces a new challenge when estimating expected life: options are almost always granted with a strike price at or near the stock price on the grant date (“at-the-money”), whereas the stock price at fiscal year end(s) and/or the vest date may not be close to the strike price. At these later measurement dates, options may be “in-the-money” (current price above the strike price) or “out-of-the-money” (current price below the strike price).
Most companies that use the Black-Scholes model for valuing options use an expected life based on either historical employee exercise behavior or the “simplified method” outlined in SAB Topic 14.D.2, whereby expected life equals the midpoint of i) the weighted average time-to-vest of the option and ii) the full contractual term of the option. The simplified method was provided as a path for companies without sufficient historical employee exercise data, but Topic 14.D.2 specifically notes that the simplified method is only applicable for options that are granted at-the-money.
Example – Case Study
Let’s examine two (2) similar companies, both of which grant options with 2-year cliff vesting and a contractual term of 10 years, however one with a grant-date expected life of 4.50 years (as determined from historical behavior), and a second at 6.00 years (based on the simplified approach).
| Company A | Company B | |
| Grant Date | 1/1/2022 | |
| Vest Date | 1/1/2024 | |
| Expiration Date | 1/1/2032 | |
| Expected Life on Grant Date | 4.50 | 6.00 |
| Implied Exercise Date | 6/30/2026 | 1/1/2028 |
Expected Life on Future Re-measurement Date (when Stock Price Does Not Equal Strike Price)
Under the new Pay Versus Performance rules, companies A and B will each need to revalue these awards at the end of their fiscal year(s) and the vest date(s). At these valuation dates, the stock price will likely no longer equal to the strike price.
As we seek to estimate the expected life of the options at these various measurement dates, we should consider the following:
- The expected life as of the grant date (whether based on historical experience or simplified method) already considers that no options will be exercised prior to vesting.
- The Society of Actuaries (SOA) research on employee exercise notes that “the rate of voluntary option exercise is strongly positively related to the level of the stock price”. In other words, the higher the stock price compared to the strike price, the shorter the expected life.
- ASC Topic 718 notes that “deeply out-of-the-money” options will have a derived service period, implying that they are subject to risk of forfeiture before reaching the money, and implying a longer expected life than an option that is “at-the-money”.
Using these principles, we can conclude the following:
Scenario | Stock Price onValuation Date | General Expected Exercise | Company A | Company B |
| Scenario 1 | = Strike Price | Equal to original expected exercise date | 6/30/2026 | 1/1/2028 |
| Scenario 2 | > Strike Price | Prior to original expected exercise date | Before 6/30/2026 | Before 1/1/2028 |
| Scenario 3 | < Strike Price | Later than original expected exercise date | After 6/30/2026 | After 1/1/2028 |
Scenario 1: Expected Life on Remeasurement Date – At-the-money Options
If the options are still at-the-money on the valuation date (the fiscal year end or the vest date), then there isn’t any reason to update the original expected exercise date. It was known at grant that the options would not be exercised prior to the vest date, so the fact that the options are still outstanding is rather unremarkable. Since the expected exercise date has not changed, the expected life as of the vest date should equal i) the expected life as of the valuation date minus ii) the vesting period. The table below shows the expected life calculation for Company A and Company B on the vest date (2.00 years after grant, or 1/1/2024).
| Company A | Company B | |
| Expected exercise date | 6/30/2026 | 1/1/2028 |
| Original Expected Life | 4.50 years | 6.00 years |
| Vesting Period | 2.00 years | 2.00 years |
| Expected Life on Vest Date | 2.50 years | 4.00 years |
Scenario 2: In-the-money Options on the Remeasurement Date
If the options are in-the-money on the valuation date, the expected life should be shorter. The next logical question becomes “how much closer?”.
In Appendix A, we illustrate an approach to determine at what “money-ness” level that exercise becomes a certainty. Following this approach, we find in our example prior that exercise is anticipated to occur when the stock price is equal to 300% of the exercise price (2x multiple), which creates a “Lower Bound” on the expected life. The “Upper Bound” has already been determined as the original expected life on the date of grant.
| Upper Bound | Interpolated | Lower Bound | |
| Stock Price | Equal to strike price | 1.5x strike price | 3x strike price |
| Expected Life on Vest Date | 2.50 years | 1.875 years | 0.00 years |
| Expected Exercise Date | 6/30/2026 | 11/15/2025 | 1/1/2024 |
Through simple interpolation, we can then determine an expected life for Company A. For “in-the-money” awards, this expected life (developed under what we’ll call the “Exercise Certainty Interpolation” as explained in the Appendix) is shorter than the lives that were outlined in Article 1. As a result, the fair value estimate is lower than the fair value estimated with other approaches.
| Methodology | Exercise Certainty Interpolation Approach | Rev. Proc. 98-34 | Half of Remaining Term | Rev. Proc. 2003-68 |
| Current Stock Price | $150 | $150 | $150 | $150 |
| Strike Price | $100 | $100 | $100 | $100 |
| Risk-Free Rate | 3.00% | 3.00% | 3.00% | n/a |
| Volatility | 30.00% | 30.00% | 30.00% | Low |
| Dividend Yield | 1.00% | 1.00% | 1.00% | n/a |
| Expected Life | 1.875 | 3.600 | 4.000 | n/a |
| Black-Scholes Fair Value | $56.11 | $62.04 | $63.24 | $76.80 |
| BS as Percent of Stock Price | 37.40% | 41.36% | 42.16% | 51.20% |
Scenario 3: Out-of-the-money Options on the Remeasurement Date
When the stock price on the valuation date is lower than the strike price, the expected exercise date should move towards the full contractual term. However, the answer to “how much closer” is a little more complicated, as the answer will be sensitive to factors like how far out-of-the-money the options are, the expected volatility of the company, and the expected post-vesting termination rate of the company. Certainly, the absolute upper bound would be setting the expected life equal to the full remaining contractual term, but this likely overestimates the expected life. If your company runs into this scenario, Infinite Equity can help develop an expected life based on the relevant factors.
Conclusion
Estimating the expected life of options that are not at-the-money is a new challenge for most companies that will need to be addressed when making disclosures under the new Pay Versus Performance rules. Some of the existing methodologies for estimating expected life or fair value can overstate the life and fair value, leading to higher than necessary compensation expense totals. As seen in the valuation table above, this impact can be significant, as some approaches may increase the compensation expense associated with outstanding or vesting options by 10% to 40%.
At Infinite Equity, we’re continuing to analyze the new Pay Versus Performance rules to help our clients navigate them with a strategy that is in full alignment with their unique needs and goals. To learn more about option valuation or estimating expected life in compliance with the new SEC rules, reach out to us at Infinite Equity today.
Appendix A: Determining Exercise Price Certainty
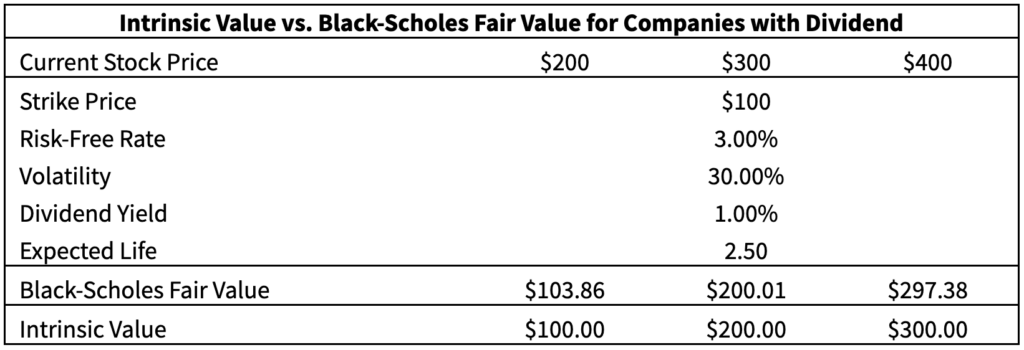
For Dividend Paying Stocks: A good place to start is to figure out when an employee would exercise immediately upon vesting, yielding an expected life of 0.00 and a fair value equal to the intrinsic value (spread between current price and strike price). Employees would exercise immediately when the present value of expected future dividends exceeds the expected future gain from the option. This point depends on the current risk-free rate, volatility, and dividend yield of the company, but generally occurs when the stock price reaches 2x to 5x the strike price. Below, we can see that the intrinsic value of an option for a company with $100 strike price, 30% volatility, and 1% dividend yield surpasses the Black-Scholes value of the option when the stock price gets to ~$300, or 3x the strike price of $100.
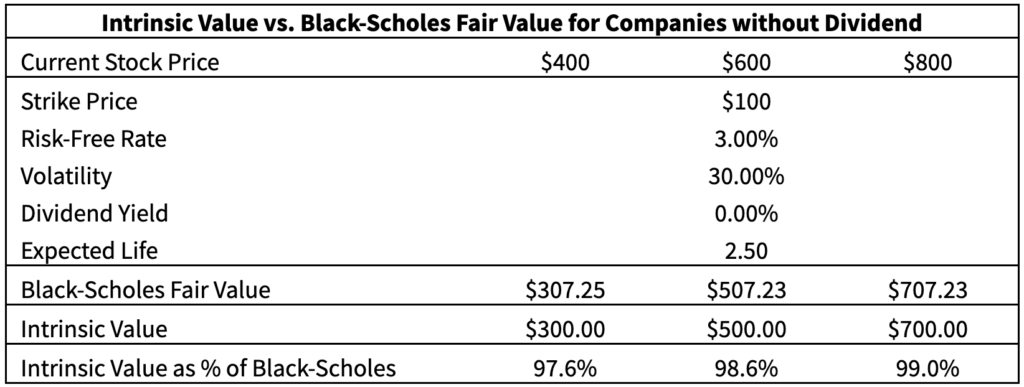
For non-dividend Paying Stocks: For companies without a dividend payment, the value of expected future dividends is $0, so the expected life would never truly go to 0.00. However, the fair value of the options becomes so insensitive to expected life at certain prices that employees would likely exercise immediately. For non-dividend paying companies, it is likely fair to assume an expected life of essentially 0.00 when the stock price reaches 4x to 8x the strike price. The table below shows that the intrinsic value approaches the Black-Scholes fair values at high strike price multiples.

The New Rules of Pay Versus Performance


